Hawking energy
The Hawking energy or Hawking mass is one of the possible definitions of mass in general relativity. It is a measure of the bending of ingoing and outgoing rays of light that are orthogonal to a 2-sphere surrounding the region of space whose mass is to be defined.
Contents |
Definition
Let  be a 3-dimensional sub-manifold of a relativistic spacetime, and let
be a 3-dimensional sub-manifold of a relativistic spacetime, and let  be a closed 2-surface. Then the Hawking mass
be a closed 2-surface. Then the Hawking mass  of
of  is defined[1] to be
is defined[1] to be
where  is the mean curvature of
is the mean curvature of  .
.
Properties
In the Schwarzschild metric, the Hawking mass of any sphere 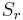 about the central mass is equal to the value
about the central mass is equal to the value  of the central mass.
of the central mass.
A result of Geroch[2] implies that Hawking mass satisfies an important monotonicity condition. Namely, if  has nonnegative scalar curvature, then the Hawking mass of
has nonnegative scalar curvature, then the Hawking mass of  is non-decreasing as the surface
is non-decreasing as the surface  flows outward at a speed equal to the inverse of the mean curvature. In particular, if
flows outward at a speed equal to the inverse of the mean curvature. In particular, if 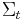 is a family of connected surfaces evolving according to
is a family of connected surfaces evolving according to
where  is the mean curvature of
is the mean curvature of 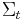 and
and  is the unit vector opposite of the mean curvature direction, then
is the unit vector opposite of the mean curvature direction, then
Hawking mass is also monotonically increasing for the inverse mean curvature flow.[3]
Hawking mass is not necessarily positive. However, it is asymptotic to the ADM[4] or the Bondi mass, depending on whether the surface is asymptotic to spatial infinity or null infinity.[5]
See also
References
- ^ Page 21 of Schoen, Richard, 2005, "Mean Curvature in Reimannian Geometry and General Relativity," in Global Theory of Minimal Surfaces: Proceedings of the Clay Mathematics Institute 2001 Summer School, David Hoffman (Ed.), p.113-136.
- ^ Geroch, Robert. 1973. "Energy Extraction." DOI: 10.1111/j.1749-6632.1973.tb41445.x.
- ^ Lemma 9.6 of Schoen (2005).
- ^ Section 4 of Yuguang Shi, Guofang Wang and Jie Wu (2008), "On the behavior of quasi-local mass at the infinity along nearly round surfaces".
- ^ Section 2 of Shing Tung Yau (2002), "Some progress in classical general relativity," Geometry and Nonlinear Partial Differential Equations, Volume 29.
- Section 6.1 in Szabados, László B. (2004), "Quasi-Local Energy-Momentum and Angular Momentum in GR", Living Rev. Relativity 7, http://www.livingreviews.org/lrr-2004-4, retrieved 2007-08-23


